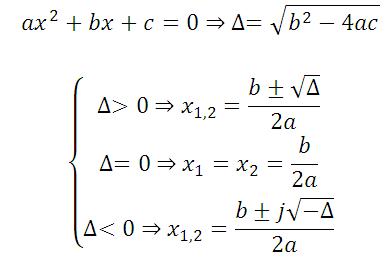
صورت کلی معادله‌ی درجه 2 به شکل ax2 + bx + c = 0 می‌باشد. برای این که معادله‌ی درجه 2 تشکیل شود، باید a != 0 و b,c عضو اعداد حقیقی باشند.

روش‌های حل معادله درجه 2

1)      روش تجزیه

 

2)      روش رسم نمودار

 

3)      روش مربع کامل کردن

 

4)      روش دلتا (روشی کلی)

 

نکته : تعداد جوابهای هر معادله، حداکثر به تعداد درجه‌ی آن معادله می‌باشد.

 

1)      در روش تجزیه، در صورت امکان، معادله‌ی درجه 2 را به گونه‌ای تجزیه می‌کنیم که معادلات درجه 1 حاصل شود و سپس آن‌ها را حل می‌کنیم تا پاسخ معادله‌ی درجه 2 به دست آید.

 

2)      در روش رسم نمودار، جمله‌ای را که توان 2 دارد در یک طرف تساوی نگه داشته و بقیه‌ی جملات را به طرف دوم منتقل می‌کنیم. سپس نمودار هر دو طرف تساوی را در دستگاه مختصات رسم می‌کنیم. تعداد نقاط تلاقی سهمی با خط راست، برابر تعداد جواب‌های معادله است.

 

نکته : روش رسم نمودار برای تعداد جواب‌ها مناسب است و جواب‌ها را به طور دقیق برای ما مشخص نمی‌کند.

 

3)      مراحل حل معادله به روش مربع کامل کردن، در زیر آمده‌است :

 

الف ) –b/2a را به دست می‌آوریم.

 

ب ) عدد به دست آمده را به توان 2 می‌رسانیم.

 

ج ) عدد حاصل از مرحله‌ی (ب) را به معادله اضافه و از آن کم می‌کنیم.

 

د ) به کمک اتحاد مربع دو جمله‌ای، معادله را حل می‌کنیم.

 

نکته : هرگاه ضریب x2 مجذور کامل نبود، همه‌ی جمله ها را بر آن تقسیم می‌کنیم تا از بین برود.

 

4)      در روش کلی در معادله‌ی ax2 + bx +c = 0، از فرمول‌های زیر استفاده می‌کنیم.

 

 B2 – 4ac         ,                 = ∆

  x1 = ( -b + √∆ )/2a        ,        x2 = (-b - √∆ )/2a